初中数学中哪些证明题比较有趣,为大家分享一个题目的多种证法!
初中数学学习中,会有很多的证明题,这些题目是初中数学学习的重点,需要学生们重点掌握,那么在这些数学题目中,学生们怎样去更好的证明呢?一个题目可以有很多的证明方法,其中很多证明的过程是有趣的,所以学生们需要更好的了解,学习更多的初中数学证明题目解题方法,详情大家了解一下吧!

罗曼罗兰曾说过:这世上并不缺乏美,缺乏的是发现美的眼睛。数学证明也是如此,如果说数学证明没有趣味,那多半是因为还没发现有趣的证明方法。
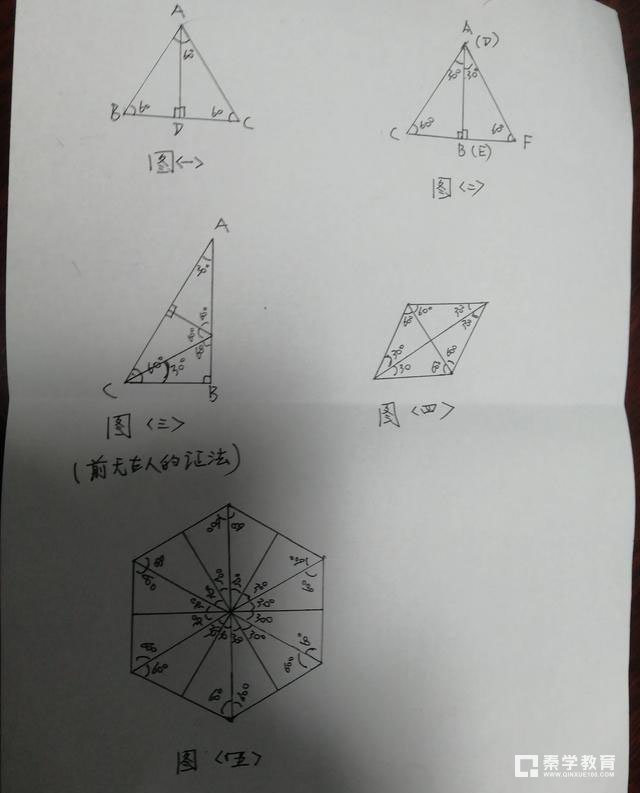
初中数学教材中,在证明“直角三角形中3O度锐角所的边的长度等于斜边长一半”这个性质定理时,是利用等边三角形三边相等三角相等且各为60度以及等腰三角形三线合一这些性质。如本文图(一)所示,首先,以等边三角形任意一条边为底边,毫无疑问,两腰是相等的,从而构成等腰三角形;其次,根据等腰三角形三线合一的性质,可知底边上的高、中线和顶角的平分线三线合一,即这个三线合一的“线”,把等边三角形分成了“含有30度锐角的两个相等直角三角形”,从而得出“直角三角形中,3O度锐角所对的边的长,等于等边三角形边长的一半,也即等于斜边长的一半”。
如果换一种证法,则要有趣一些,如本文中图(二)。将含有30度锐角的两个全等直角三角形ABC和DEF的较长的直角边AB和DE重合,则可组合成一个等边三角形ACF。根据等边三角形全边相等的定义,再根据三点共线的条件,可知C、B、E、F四点共线;从而可知,含3O度锐角所对的边的长等于等边三角形ACF的边的一半,即等于其斜边长的一半。
如果再换一种证法,则更加有趣,如图(三)。这种证法很可能是前无他人的一种证法,即是本人的独创,这种证法的有趣在于:用含有30度锐角的三个全等三角形,拼成一个含有30度锐角的大直角三角形,从而构成四个含有30度锐角的三角形,的好玩。具体证法还可以有另外一种描述:在含有3O度锐角的直角三角形中,作6O度锐角的平分线交其对边于一点,过该点作斜边的垂线,很容易证明,该垂线和6O度的平分线将大直角三角分割为三个全等的含30度锐角的直角三角形。由此即可证明“直角三角形中3O度锐角所对的直角边等于斜边的一半”。
含3O度锐角的直角三角形,可视为一个单元图形。在初中平面几何中还可以组成两个比较特殊的图形,有一组对角为60度的菱形和正六边形。菱形由4个这样的全等三角形组成,正六边形由12个这样的全等三角形组成。这样分割之后。这两个图形的性质很容易得证,也比较有趣好玩。如本文中图(四)和图(五)。
再比如。初中代数中的三个恒等式:两数和的平方、两数差的平方、两数的平方差。如果只用乘法的分配律和因式分解的知识来理解和证明,则显得比较枯燥;而如果借助正方形的面积和数形结合的方法,则比较有趣些。
在本文附图(六)中,(a十b)的平方,就是边长为a十b的大正方形的面积,它等于两个长方形(1)与(2)的面积之和,加上一个正方形(3)的面积之和。(1)的面积是a(a+b),(2)的面积是ab,(3)的面积是b的平方。相加后展开再合并即可得证。
其它两个恒等式也可用似类的方法得证。如本文图(七)和图(八)。
- 热门课程
- 热门资讯
- 热门资料
- 热门福利
-
 西安龙门补习学校怎么样?管理严格不?在选择补课学校的时候,很多学生和家长会从两个方面来考察学校的情况,如学校的管理是否严格、学校的实力是否足够。今天小编就跟着大家一起来聊聊西安龙门补习学校怎么样?管理严格不?希望能对大家有帮助。 西安龙门补习学校怎么样? 西安龙门补习学校是在中高考补习届深耕二十多年的老牌机构,已经有很成熟的办
西安龙门补习学校怎么样?管理严格不?在选择补课学校的时候,很多学生和家长会从两个方面来考察学校的情况,如学校的管理是否严格、学校的实力是否足够。今天小编就跟着大家一起来聊聊西安龙门补习学校怎么样?管理严格不?希望能对大家有帮助。 西安龙门补习学校怎么样? 西安龙门补习学校是在中高考补习届深耕二十多年的老牌机构,已经有很成熟的办 -
 初三物理成绩差怎么办?西安伊顿教育一对一课程能有效果吗?很多初三学生物理成绩不是很好,想提升却不知道如何下手,那选择补课班是一种很好的方式,听说西安伊顿教育还不错,那它的一对一课程能有效果吗?有没有什么初三物理成绩差的提升方法呢?本文将跟大家详细聊聊这两个问题,希望对大家有帮助。 初三物理成绩差怎么办? 物理这个科目的知识点虽然很多、逻辑性也很强
初三物理成绩差怎么办?西安伊顿教育一对一课程能有效果吗?很多初三学生物理成绩不是很好,想提升却不知道如何下手,那选择补课班是一种很好的方式,听说西安伊顿教育还不错,那它的一对一课程能有效果吗?有没有什么初三物理成绩差的提升方法呢?本文将跟大家详细聊聊这两个问题,希望对大家有帮助。 初三物理成绩差怎么办? 物理这个科目的知识点虽然很多、逻辑性也很强 -
 初三去全封闭补课学校好不好?秦学伊顿补习学校值得去吗?初三这个阶段对于很多学生和家长来说是非常关键的,很多家长都在为孩子的成绩焦虑,想帮助孩子快速的提升成绩,所以就有很多的家长考虑让孩子参加全封闭补课学校,那初三学生去全封闭补课学校好不好呢?秦学伊顿补习学校还值得大家去吗?本文将跟大家详细聊聊这两个问题,希望对大家有帮助。 初三去全封闭补课学校好
初三去全封闭补课学校好不好?秦学伊顿补习学校值得去吗?初三这个阶段对于很多学生和家长来说是非常关键的,很多家长都在为孩子的成绩焦虑,想帮助孩子快速的提升成绩,所以就有很多的家长考虑让孩子参加全封闭补课学校,那初三学生去全封闭补课学校好不好呢?秦学伊顿补习学校还值得大家去吗?本文将跟大家详细聊聊这两个问题,希望对大家有帮助。 初三去全封闭补课学校好 -
 西安伊顿教育有高三冲刺班吗?高三学生基础不好怎么学呢?高三的很多学生在复习阶段出现很多的问题,在这个阶段学生如果基础知识掌握的不扎实,在考试中是很难取得好成绩,那想要获得好的学习方法成为了大家关注的重点,小编今天就跟大家详细聊聊“高三学生基础不好怎么学呢?西安伊顿教育有高三冲刺班吗?”这两个问题,希望能对大家有帮助。 高三学生基础不好怎么学呢?
西安伊顿教育有高三冲刺班吗?高三学生基础不好怎么学呢?高三的很多学生在复习阶段出现很多的问题,在这个阶段学生如果基础知识掌握的不扎实,在考试中是很难取得好成绩,那想要获得好的学习方法成为了大家关注的重点,小编今天就跟大家详细聊聊“高三学生基础不好怎么学呢?西安伊顿教育有高三冲刺班吗?”这两个问题,希望能对大家有帮助。 高三学生基础不好怎么学呢?
-
 清华大学1933年高考试卷什么样?8个科目仅一张考卷,且仅有8道题说起清华大学,那还真不是一般的难考呀,翻看往年的录取分数线,我们不难发现除了个别特殊的省份外,较低都在600以上呢,这么高的分数恐怕只有各省较好高中的尖子生才能进去吧! 如果想获取更多学校资讯、学校轶事、大学、学习资料以及自主招生方面相关的信息,小鱼老师分享大家去关注考学校公众
清华大学1933年高考试卷什么样?8个科目仅一张考卷,且仅有8道题说起清华大学,那还真不是一般的难考呀,翻看往年的录取分数线,我们不难发现除了个别特殊的省份外,较低都在600以上呢,这么高的分数恐怕只有各省较好高中的尖子生才能进去吧! 如果想获取更多学校资讯、学校轶事、大学、学习资料以及自主招生方面相关的信息,小鱼老师分享大家去关注考学校公众 -
 观神州十三号发射直播有感 神州十三号发射观后感作文最近我们航天事业频频传来喜报,神州十三号又成功发射了。不知道大家有没有去观看直播呢?相信咱们看了直播的心中一定是无比激动和自豪,大家也有想说话来表达自己激动的心情,这里呢就有几篇是关于观看神州十三号发射的观后感,我们来看看大家都是怎样形容自己的心情的。 观神州十三号发射直播有感 神州十三号发射
观神州十三号发射直播有感 神州十三号发射观后感作文最近我们航天事业频频传来喜报,神州十三号又成功发射了。不知道大家有没有去观看直播呢?相信咱们看了直播的心中一定是无比激动和自豪,大家也有想说话来表达自己激动的心情,这里呢就有几篇是关于观看神州十三号发射的观后感,我们来看看大家都是怎样形容自己的心情的。 观神州十三号发射直播有感 神州十三号发射 -
 观《长津湖》有感作文 电影长津湖观后感近期热映电影《长津湖》让我们每个人的心灵震撼,这部电影讲述了抗美援朝时期的战争,在电影院看这部电影的观众们无一不是感动到热泪,走出影院的步伐也是沉重的。《长津湖》反映了抗美援朝时期的中国人民志愿军为捍卫祖国,保家卫民浴血战场,我们来看大家对这部影片看完后的感想,分享几篇电影长津湖观后感作文给到你
观《长津湖》有感作文 电影长津湖观后感近期热映电影《长津湖》让我们每个人的心灵震撼,这部电影讲述了抗美援朝时期的战争,在电影院看这部电影的观众们无一不是感动到热泪,走出影院的步伐也是沉重的。《长津湖》反映了抗美援朝时期的中国人民志愿军为捍卫祖国,保家卫民浴血战场,我们来看大家对这部影片看完后的感想,分享几篇电影长津湖观后感作文给到你 -
 孟晚舟回国作文素材 孟晚舟高考热点写作角度最近孟晚舟回国的消息另大家振奋,经历这么长时间的家,她终于要回来了,相信各方都在努力争取孟晚舟女士能够早日回国。终于我们的努力没有白费,孟晚舟女士终于回到了祖国母亲的怀抱。如果将其作为高考的热点,可能会出现在作文当中,下面分享关于孟晚舟女士回国事件主题的写作角度和作为素材。 主题:孟晚舟回国
孟晚舟回国作文素材 孟晚舟高考热点写作角度最近孟晚舟回国的消息另大家振奋,经历这么长时间的家,她终于要回来了,相信各方都在努力争取孟晚舟女士能够早日回国。终于我们的努力没有白费,孟晚舟女士终于回到了祖国母亲的怀抱。如果将其作为高考的热点,可能会出现在作文当中,下面分享关于孟晚舟女士回国事件主题的写作角度和作为素材。 主题:孟晚舟回国


















 All right reserved
All right reserved
