初中数学需要学习很多的知识点，这些知识点是学生们后期学习的关键，是学生们学习中需要重点了解的内容，初中的数学其实并不难，但是却很重要，只有学好了初中的知识点，学会灵活运用，才能适应高中的学习，跟上高中的进度，更好的理解高中的知识，所以学好初中数学，学生们还有很多需要明确的事情，那么关于初中各部分知识点的学习以及技巧分享给学生们大家可以了解看看。

　　由于初中数学的特殊性，只能将初中数学的学习方法尽量精简的分析一下。

　　我认为初中数学和小学数学学习的方法和对思维的要求有很大的区别。

　　小学数学模块化明显，可以寻找方法，逐个击破。初中数学各环节联系紧密，初中各个环节相互影响的特征明显。

　　几乎每个部分都能影响整个初中数学和高中数学的学习，给学生造成了比较大的思想负担。

　　要学好初中数学，就需要仔细分析整个初中数学的知识体系，做到心里有数。

　　一、“数”和“式”。

　　A.数

　　初中的“数”其实是实数，其中又分为有理数和无理数。这部分想学好是不难的，无非是把小学的整数分成正负，小学的分数也分成正负，再加上无限不循环小数(无理数)。并在这个基础上衍生出了：值、平方根、立方根等一些基础概念。

　　不管是网上还是各种辅导书上很容易能找到一种大括号图，一张图罗列全部初中的数。

　　“数”的部分两个关键： 1.记准概念。 2.正确理解运算。

　　第一条不用讨论，第二条要解释一下，什么叫运算?我认为，初中的“运算”是小学“计算”的升级版，不仅要计算数，还要区别正负号、变号、值运算、根号运算。听起来很复杂，其实很简单，就是比小学时多注意一些，多了几种运算规则而已。增加的练习量，就可以达到运算了。

　　“数”的部分要扎实，要达到运算，因为后面还要上升到各种“式”的运算，还有幂运算，所以这部分达不到运算后面就很麻烦。只有一个办法，严格执行前文两个“关键”，然后增加练习量，直到达到“运算”不出错。

　　B.式

　　没有喘息的机会，运算紧接着就会进入“式”时代。迎来了一位“新朋友”——代数式。又按形式分为：整式和分式，其中整式还包括：单项式、多项式。

　　首先，分清楚各种是“式”，然后遵循前文的“运算”，开始进行“式的运算”，这时主要“难度”就来了——“式的乘除”、“幂运算”、“式的约分”，但其实这种难度仔细分析的话，其实是新的形式，旧的运算思路，掌握起来不算困难。

　　接着，分解因式(化多项式为几个整式的积)，这又难住了很多学生，在这部分学校老师讲的很多了，我就总结一下用的方法，其实也是一种种题型的解法。

　　整式四种方法： 1.提公因式法 2.运用公式法 3.分组分解法 4.十字相乘法

　　(公式法主要：平方差公式/完全平方公式)

　　分式三个注意：1.掌握分式的性质

　　2.分式的通分和“加减运算”

　　3.分式方程，分母不能为零，“增根”要剔除。

　　二、方程(组)和不等式(组)

　　方程部分：一元一次方程，二元一次方程组。

　　不等式部分：一元一次不等式，一元一次不等式组。

　　一元一次方程：去分母，移项，合并同类项。

　　要注意通过“幂运算”把未知数系数化为1。

　　二元一次方程组：代入消元法/加减消元法。

　　注意理解代入和消元的道理，在这个过程中，注意学会写解方程组的过程，合理地写明“代入”、“得”之类的过程，解方程组形式上就变得简单多了。(因为不用写计算过程，嘿嘿)

　　注意：不等式(组)基本思路和方程(组)是一样的。但需要注：1.不等号方向问题。2.解的表达形式也和方程(组)有区别。

　　三 一次函数

　　基础部分，一图了然，注意要理解性记忆，不能死记，理解了，自然就记住了。

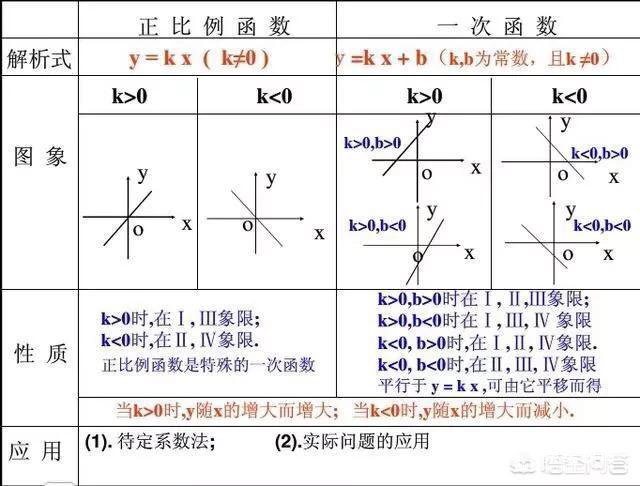
　　经验：求一次函数的表达式，基本和二元一次方程组关系很大，思路也基本一致，只不过“x和y”变成“k和x”而已，注意“两点确定一条直线”在这里很好用哦。

　　个人经验：1.若关系式已知，点的横纵坐标都可以互求。

　　2.若要求关系式，需要先得到两个点的坐标。

　　四、一元二次方程：四方法、理、一判别

　　四方法(题型)

　　配方法

　　分解因式法

　　公式法(这里指的是分解因式中的公式法)4.十字相乘。

　　理

　　韦达定理：利用韦达定理，可以求出一元二次方程中的各系数，在题目中很常用。

　　根的判别

　　当△>0时，一元二次方程有2个不相等的实数根;

　　当△=0时，一元二次方程有2个相同的实数根;

　　当△<0时，一元二次方程没有实数根。

　　五 二次函数(二次函数和一元二次方程关系很密切，的哥俩好!)

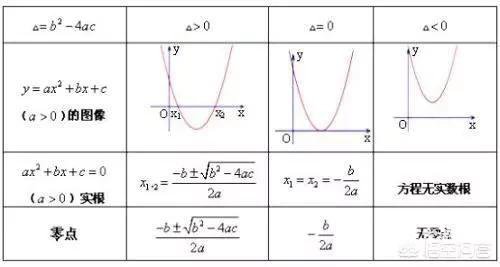
　　这张图就包含了二次函数的基本性质了，也是需要记住的东西。

　　特别提一下前面一元二次方程的知识在二次函数图像上的都可以对应。

　　除此之外，还要知道各个系数和图像的关系，韦达定理在这里也很重要，可以找到图像顶点、对称轴，还可以求二次函数的表达式，是常用的，是解决很多问题的关键。

　　几何部分

　　终于来到了几何部分，终于马上回答完了!

　　为什么说马上答完了呢?因为几何部分主要讲一个字：“背”!的经验干货，的学习精髓!

　　因为几何虽然有很多图形和知识，但是总体我分享一种学习好初中数学的方法。

　　从点、线、面到三角形、各种四边形、圆形……

　　请记住一句话：在理解的基础上，把各种图形的定义、性质、公式、定理、推论、判定全部记住，全部记住!!!

　　没商量，学到哪部分就背哪部分，要能做到自己画图，来说明定义、性质、公式、定理、推论、判定、法则……

　　有人说数学不能死记硬背，我不反对，但几何的学习，在理解的基础上，全部背过!然后在进行相关练习，你会发现有突飞猛进的效果!!!

　　就算到了高中，平面几何和立体几何也要都是这样学较快，较有效率!

　　这里注意一下：画图理解的过程并不难，也不需要太多指导，全在课本上。练习也无需做太多额外练习，就跟着学校老师，边学边背边练，学校的习题卷子足矣，更不需要找培训班。(当然已经落下来的，还是需要在假期找家教或者辅导班。